Obesity and anesthetic pharmacology: simulation of target-controlled infusion models of propofol and remifentanil

Obesity and anesthetic pharmacology

Article information

Korean J Anesthesiol. 2021;74(6):478-487

Publication date (electronic) : 2021 August 18

Department of Anesthesia and Pain Medicine, Pusan National University School of Medicine, Busan, Korea

Corresponding author: Tae Kyun Kim, M.D., Ph.D. Department of Anesthesia and Pain Medicine, Pusan National University School of Medicine, 20 Geumo-ro, Mulgeum-eup, Yangsan 50612, Korea Tel: +82-55-360-2756 Fax: +82-55-360-2149 Email: anesktk@pusan.ac.kr

Received 2021 August 9; Accepted 2021 August 17.

Abstract

The prevalence of obesity is increasing, resulting in an increase in the number of surgeries performed to treat obesity and diseases induced by obesity. The associated comorbidities as well as the pharmacokinetic and pharmacodynamic changes that occur in obese patients make it difficult to control the appropriate dose of anesthetic agents. Factors that affect pharmacokinetic changes include the increase in adipose tissue, lean body weight, extracellular fluid, and cardiac output associated with obesity. These physiological and body compositional changes cause changes in the pharmacokinetic and pharmacodynamic parameters. The increased central volume of distribution and alterations in the clearance of drugs affect the plasma concentration of propofol and remifentanil in the obese population. Additionally, obesity can affect pharmacodynamic properties, such as the 50% of maximal effective concentration and the effect-site equilibration rate constant (ke0). Conducting a simulation of target-controlled infusions based on pharmacokinetic and pharmacodynamic models that include patients that are obese can help clinicians better understand the pharmacokinetic and pharmacodynamic changes of anesthetic drugs associated with this population.

Keywords: Cardiac output; Computer simulation; Ideal body weight; Metabolic clearance rate; Obesity; Pharmacokinetics

Introduction

The prevalence of obesity is increasing annually worldwide. According to the WHO report [1], 13% of the world’s adult population is obese, and the number has been growing steadily. In 2016, obesity was approximately three times what it was in 1975. In particular, the morbidly obese population, with a body mass index (BMI) > 40 kg/m², is on the rise. Given the increase in the number of surgeries performed to treat obesity and associated diseases and the comorbidities present in this population, anesthesiologists are having an increasingly difficult time managing these patients. During surgery, anesthesiologists may have trouble with intubation and airway management before and after surgery, mechanical ventilation, control of diabetes and hypertension, obstructive sleep apnea, and cardiopulmonary disease.

In addition, pharmacokinetic and pharmacodynamic changes of anesthetic drugs in obese patients make it difficult to control the appropriate dose of anesthetic agents. The increase in body mass and changes of its composition influences pharmacokinetic parameters such as distribution volume, clearance, and elimination half-life. Comorbidities in obese patients, such as obstructive sleep apnea, may also cause narrowing of the therapeutic dynamic range of anesthetic drugs.

This review will include a discussion about the changes in various anesthetic drugs’ pharmacokinetic and pharmacodynamic behaviors that result from the increase in body mass and compositional changes that occur in obese patients based on published articles.

Changes in body mass composition

In obese individuals, the lean body mass, which includes vessel-rich organs and the tissues where drugs act, does not usually increase proportionally to the increase in total body mass. Rather, as the body weight increases, the blood volume, fat mass, lean body mass, and extracellular water volume increase along with the increase in total body weight (TBW); however, the composition of the mass does not always increase in proportion to the total body mass. The fat mass tends to increase along with the TBW; however, lean body mass does not. The ratio of lean body weight (LBW) to TBW decreases as the TBW increases. The proportion of LBW, which explains the increase in TBW, is approximately 20%–40% [2].

When a drug dosage is determined, it is usually scaled based on the TBW. However, administering drugs scaled simply using the TBW in obese patients would result in an overdose. Therefore, obese individuals need other mass scalars to calculate the appropriate dose, such as LBW, ideal body weight (IBW), and fat-free mass. Various mass scalars have been introduced, each with their own characteristic features and equations (Table 1).

Table 1.

Common Dosing Scalars

Total body weight

Dosing based on the TBW is valid for people with a normal weight. In obese patients, however, the lean tissue, which is where most cardiac output is delivered, does not increase in proportion to the TBW; therefore, the use of the TBW to determine the dose in obese patients would result in an overdose. Other mass scalars must therefore be considered.

Ideal body weight

Numerous equations have been introduced to calculate the IBW [3]. The disadvantage of this mass scalar is that individuals who have the same sex and height receive the same dose regardless of obesity and body mass composition.

Lean body weight

The LBW is the body mass without fat or adipose tissue. For the past several decades, James’ equation has frequently been used to calculate the LBW [4]; however, it has serious limitations for the obese population. The equation underestimates the LBW of morbidly obese individuals and even yields a flawed negative LBW. In 2005, Janmahasatian et al. [5] suggested another equation be used to overcome the limitations of James’ formula. This equation is derived from dual-energy X-ray absorptiometry measured in men and women of various body weights and heights. Most metabolic activities occur in the lean body mass, and an increase in cardiac output is closely correlated with an increase in the LBW. Therefore, the early distribution kinetics of the drug and clearance are influenced by cardiac output.

Adjusted body weight

The adjusted body weight (ABW) is defined as the IBW plus a proportion (40%) of the excess TBW compared to the IBW. The ABW is calculated as the IBW + 0.4 × (TBW – IBW).

Body mass index

The BMI is widely used to determine the degree of obesity and is calculated as the ratio of the body weight (kg) to the height (m) squared. However, the BMI does not consider the body mass composition.

Body surface area

The body surface area (BSA) has been primarily used as a dosing scalar for chemotherapeutic agents. The equations derived by Mosteller [6] are widely used. However, the BSA does not discriminate between fat and lean body mass.

Pharmacokinetic mass

Due to the non-linear relationship between fentanyl clearance and the TBW, if fentanyl was administered based on the TBW, obese patients would be overdosed. Shibutani et al. [7] therefore devised a modified weight called pharmacokinetic mass, in which the mass scalar increases in proportion to the increase in clearance. The ‘pharmacokinetic mass’ is reported to be highly correlated with the LBW.

Allometric scaling

Allometric scaling is a method that establishes a relationship between the body mass and pharmacokinetic or pharmacodynamic parameters with a certain fixed exponent constant α, calculated as follows: Clearance = β × (TBW)^α. Alpha is usually called the allometric coefficient. Allometric scaling is designed to apply animal experiment results to humans or to assume pediatric doses from adult data [8–10]. Allometric scaling can sometimes be useful in determining the drug dosages for obese patients. However, extrapolating analyzed data out of the range, such as data from non-obese to obese populations, has inherent problems.

Changes in pharmacokinetic properties

The various physiological and anthropometric changes that occur in obese patients affect pharmacokinetic parameters, such as distribution volume and clearance, which are used to determine drug concentration and dosage. The characteristic changes in patients with obesity that affect pharmacokinetic parameters, which are not present for those with a normal weight, include an increase in lean body mass, muscle mass, fat mass, circulatory blood volume, and total body water. In addition, changes in the lipophilicity or hydrophilicity and protein binding of drugs affect pharmacokinetic parameters in obese patients [11,12].

The increase in fat mass associated with obesity increases the distribution volume of lipophilic drugs [13-15]. In a study of thiopental, which has high lipophilicity, the steady-state distribution volume and the elimination half-life in obese patients was found be considerably higher. [16]. A study of propofol also showed that the volume of distribution increases in proportion to the increase in the TBW [17]. While the volume of distribution of this lipophilic drug does increase as fat mass increases, it does not increase proportionally. The reason for this is related to changes in blood flow to the adipose tissue, which accounts for 5% of cardiac output in non-obese patients, but it is reduced to 2% in obese patients [18].

The increase in the central volume of distribution associated with obese individuals leads to a rapid decrease in concentration during the initial distribution phase. The loading dose is mainly determined by the size of the central volume of distribution, which determines the changes in the initial concentration after administration. In addition, the increase in cardiac output, which is a commonly observed physiological change in obese patients, is another factor explaining low plasma concentrations in the distributive period [19,20].

Increased cardiac output plays an important role in the increase in the overall clearance of drugs, thus lowering the elimination half-life of the drug. The increase in cardiac output in patients with obesity is highly correlated with the increase in the LBW [21,22]. Increased cardiac output and increased LBW are associated with increased renal and hepatic blood flow, which in turn increase the overall clearance and initial distributive clearance [23,24].

The increase in cholesterol levels and free fatty acids in obese patients has been found to inhibit the binding of drugs to plasma proteins, such as albumin. There is also a disagreement, however, as binding of the drug to plasma proteins increases due to increased levels of α-acid glycoproteins in obese patients [25-28].

Changes of pharmacodynamic properties

Excess fat caused by obesity leads to disturbances in body metabolism and inflammatory reactions and increases drug sensitivity [29,30]. Some studies have shown that obesity increases pain sensitivity, while other studies have found no adverse or pharmacodynamic effects [31-33]. Cortinez et al. [34] did not find any changes in the pharmacodynamic parameters in obese patients. Dong et al. [35], however, reported a decrease in the 50% of maximal effective concentration in obese patients and an increased sensitivity to propofol.

Considering that obesity affects both pharmacokinetics and pharmacodynamics, determining the dose of propofol based on the EEG processed monitor (e.g., BIS, entropy) should be considered. Subramani et al. [36] reported that the induction dose of propofol based on the BIS index was different from the induction dose based on LBW in morbid obese patients. In this study, compared to the amount of propofol administered based on the LBW, a larger amount was administered when the dose was based on the BIS. These authors also reported that for those who were administered propofol based on the LBW, 60% of them required an additional dose of propofol to obtain a sufficient depth of anesthesia. The Eleveld model also suggests that the effect-site equilibration rate constant (ke0) changes as the body weight changes, using the equation 0.146 × (weight [kg] / 70)^-0.25.

Target-controlled infusion model for the obese population

Studies on a target-controlled infusion (TCI) model for the obese population have been conducted using several drugs, including propofol and remifentanil [37-42]. If the obese population was not included in the process of building a TCI model and not equipped into the anesthetic delivery pump, the exact target effect concentration cannot be obtained by calculating doses simply based on the TBW of an obese patient.

However, some reports have stated that changing the weight scalar of the known TCI model to something other than the TBW improves the performance of the model in obese patients. Cortinez et al. [43] reported an improvement in the performance of the TCI model by simply switching the original weight scalar with an alternative weight scalar. They stated that the performances of the Shnider and Marsh models were dramatically improved after substituting the TBW with the ABW. La Colla et al. [40] proposed using a fictitious height, or an adjusted height, for the Minto model to offset the inaccurate influence of the LBW when the model is applied to obese individuals.

However, these types of proposed shortcuts are not a definitive solution. Constructing a new pharmacokinetic model that includes data obtained from obese patients would be a more desirable approach. Eleveld et al. [44] and Kim et al. [42] presented integrative models for propofol and remifentanil, respectively, by gathering data from various pharmacokinetic studies that included obese patients.

Simulations

Before administering drugs to obese patients, simulations based on pharmacokinetic or pharmacodynamic models are helpful for planning drug administration. A simulation model that includes the obese population would help clinicians discover unexpected errors and prepare for them in advance. Therefore, the Eleveld and Kim models were simulated to discover the differences in the pharmacokinetics of propofol and remifentanil between obese and non-obese individuals.

It is clinically impractical to administer propofol and remifentanil independently at each target concentration without consideration of the interaction. The interaction between propofol and remifentanil, therefore, should be considered in the simulation of obese patients. The target concentration of propofol and remifentanil should be adjusted to reflect a real clinical situation in which an interaction of the drugs occurs.

For this interaction, the hierarchical model proposed by Bouillon et al. [45] was referenced. The target concentration for induction and maintenance of anesthesia was maintained at the target concentration combinations of the two drugs, achieving a rate of 95% no response to laryngoscope intubation or hypnosis (Fig. 1). The resultant predicted concentration of each drug simulated by the scenario is plotted in Fig. 2.

Fig. 1.

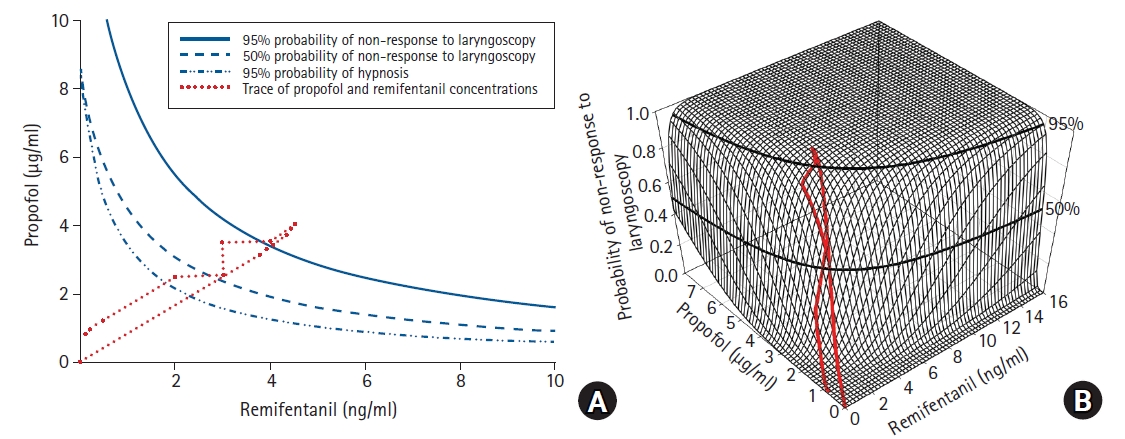
Planning of the simulation based on loss of responsiveness predictions. (A) Isoboles are presented on top-down view. Isoboles of 95% and 50% non-response to laryngoscope and hypnosis are presented. The inward bow of the isoboles indicates that the interaction is synergistic. (B) Simulated target concentrations are plotted on the interaction surface.

Fig. 2.

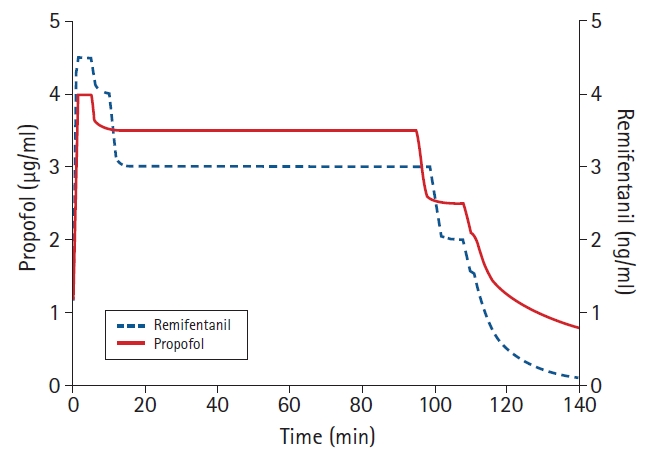
Resultant effect-site concentrations of propofol and remifentanil. Target concentration of propofol and remifentanil are predicted according to the simulated scenario.

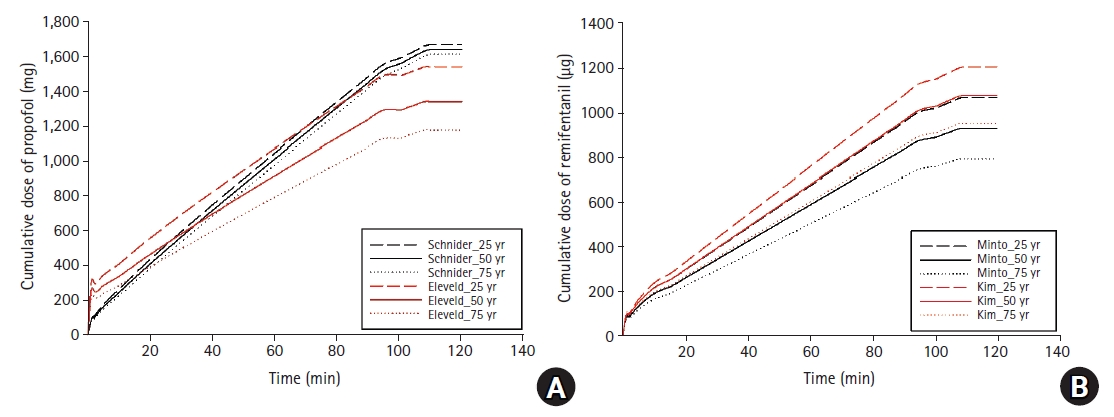
The Eleveld and Schnider models were compared for the propofol simulation, while the Minto and Kim models were compared for the remifentanil simulation. In the Eleveld model, various covariates are used to determine the pharmacokinetic and pharmacodynamic parameters. These covariates include the coadministration of opioids and the participant’s health status (patient or healthy volunteer), among others. While all cases could not be covered by this simulation, the influences of weight and age were simulated. A simulation was performed for a healthy volunteer who was administered an opioid and remifentanil and was 170 cm in height. The ke0 from the Minto model was used as a reference for the Kim model, since it does not include the ke0. The purpose of the simulation was to show the changes in the total cumulative dose and infusion rate according to various BMIs and ages.

The cumulative dose of the Eleveld model was larger than that of the Schnider model early in the TCI. This was because the Schnider model has a small and fixed central compartment volume, while the Eleveld model has a relatively larger central compartment volume, which requires a relatively larger amount of propofol at the beginning of the TCI to maintain the same target concentration (Fig. 3A).

Fig. 3.

Comparison of distribution volumes and clearance. Central volumes of distribution and clearance are compared between the pharmacokinetic models by changing the BMI. (A) Central volume of distribution changes in propofol models, (B) Clearance changes in propofol models, (C) Central volume of distribution changes in remifentanil models, (D) Clearance changes in remifentanil models. BMI: body mass index.

Later in the TCI infusion, however, the cumulative dose of the Schnider model was found to increase more than that of the Eleveld model. As the BMI increased, however, the clearance of the Schnider model increased much more than that of the Eleveld model (Fig. 3B). The explanation for this finding is that with a relatively high clearance, a higher dose of the drug is needed to maintain the same target concentration. This trend was significantly more prominent in obese than in non-obese individuals (Fig. 4A). Therefore, when TCI is performed with the same target concentration, the initial infusion rate of the Eleveld model was faster but gradually decreased over time since the clearance was lower than that of the Schnider model (Fig. 4B).

Fig. 4.

Comparison of cumulative doses and infusion rates. The cumulative doses and infusion rates are presented by altering the BMI, at a fixed age of 50 years. (A) Cumulative doses of propofol models, (B) Infusion rates of propofol models, (C) Cumulative doses of remifentanil models, (D) Infusion rates of remifentanil models. BMI: body mass index.

When the Minto and Kim models for remifentanil were compared for people with a normal BMI, the central compartment volume and clearance did not appear to be different between the models. However, as the BMI increased, the central compartment volume and clearance according to the Minto model did not increase in proportion to the BMI because the LBW of James’ equation was installed in every parameter of the Minto model. In James’ equation, LBW decreases with increasing body weight in morbidly obese individuals (Fig. 3C). However, the central compartment volume and clearance using the Kim model increased according to the increase in the BMI. The Kim model does not use James’ equation but rather applies the fat-free mass from the Janmahasatian equation, which is used to calculate the fast-peripheral compartment volume. The central compartment volume and clearance with the Kim model are generally predicted to be larger than those with the Minto model. As the BMI increased, the difference in the central compartment volume and clearance between the two models increased (Fig. 3D). Therefore, when a TCI is performed using the Kim model, the cumulative dose is predicted to be larger over time than that using the Minto model. The difference in the cumulative dose between the two models was larger in obese patients (Fig. 4C). The infusion rate was also higher in the Kim model, but both models showed similar trends throughout the simulation (Fig. 4D).

An additional simulation considering the influence of age showed that the difference in the cumulative dose of propofol between the models increased with age. In the case of remifentanil, however, the difference in the cumulative dose between the two models remained constant for all age groups (Fig. 5).

Fig. 5.

Comparison of the cumulative doses. The cumulative doses are presented by varying the age, with a fixed BMI of 45 kg/m². (A) Cumulative doses of the propofol models, (B) Cumulative doses of the remifentanil models. BMI: body mass index.

Discussion

Regardless of applying an appropriate mass scalar for induction and maintenance of anesthesia, the target concentration cannot be guaranteed by manual administration using a simple calculation of the dose. In other words, a holistic TCI device equipped with an appropriate pharmacokinetic and pharmacodynamic model is needed to control the concentration of anesthetic drugs. Drug infusions through the TCI system is theoretically the most accurate and fastest way to reach the target concentration, but it requires an accurate model to support it. Many pharmacokinetic and pharmacodynamic models, however, were created from data that did not include information of obese patients, and therefore cannot accurately predict concentrations of drug in blood in these patients. Recently, a few models have been introduced that can be applied to both obese patients and general patients [42,44].

The Eleveld model is a well-constructed model that can be used to administer more accurate concentrations of drugs to individual patients through the inclusion of various covariates relevant to actual clinical situations. Since the Eleveld model includes the use of opioids as a covariate, among others, this model may be a more practical model. When propofol is administered in clinical practice, opioids such as remifentanil are almost always administered together, and the two drugs may affect each other pharmacokinetically and/or pharmacodynamically [46]. The propofol simulation conducted for this review also included covariates for opioid use to reflect the effect of co-administration of remifentanil.

Based on the Eleveld model, the central compartment volume does not increase significantly (16.2%) with an increase in BMI. The clearance of obese patients, however, increases as the BMI or weight increases (54.9%). Clinically, this means that if propofol is administered to obese patients during anesthesia induction with a bolus dose based on the TBW, an overdose may occur because of relatively small increase of central compartment volume. In the case of continuous infusions, however, TBW could be adopted as a dosing scalar for anesthesia even for obese patient as the clearance of obese patient increase enough with the increase of TBW [17,34]. These observations are consistent with previous reports which have found that the increase in the volume of distribution is relatively small while the increase in clearance is prominent in obese [18,23,24].

Even though the best model can accurately predict concentrations, it cannot take all clinical situations into account. Pharmacokinetic changes in propofol can be influenced by various factors, such as very lean or underweight body types, laparoscopic surgery, and a prone posture [47-50]. Propofol itself can cause pharmacokinetic changes. The cardiac depression caused by propofol affects its own distribution and clearance. Therefore, rather than trying to discover every variable that may affect pharmacokinetics and create endless new models, it is essential that patients monitoring, such as the BIS, be used to confirm whether the purpose of the drug is achieved.

However, how many models are currently available for TCIs? Most commercial infusion pumps are not equipped with the new models that have been built for obese patients. To apply a new TCI model suitable for obese patients, an infusion pump must be connected to a computer with TCI software, through which a pharmacokinetic/pharmacodynamic model suitable for obese patients can be run. Another method is to apply an appropriately modified scalar instead of using the patient’s actual height or weight in the model already installed in a commercial TCI pump. Through using the ABW instead of the TBW for the traditional Schnider and Marsh models, or inputting a fictitious height for the Minto model, replacing true patient data is a possible solution; however, modified scalars are not a perfect solution.

In conclusion, simply administering an anesthetic drug based on body weight to obese patients is associated with a high risk of overdosing. Comorbidities associated with obesity can further increase the risk of overdosing. To determine the appropriate dose for obese patients, it is important to understand how the pharmacokinetics and pharmacodynamics change as the body weight increases. Factors that affect the pharmacokinetic changes in obese individuals include an increase in adipose tissue, LBW, extracellular fluid, and cardiac output.

Several mass scalars, including the IBW and LBW, have been introduced to more appropriately calculate drug dosages for obese patients; however, there are no mass scalars that can be applied to all drugs and individuals. Therefore, it is important to carefully monitor the effects and side effects of the drugs during administration.

Notes

Funding

This work was supported by a 2-year Research Grant from the Pusan National University (201911630003).

Conflicts of Interest

No potential conflict of interest relevant to this article was reported.

References

1. WHO. Obesity [Internet]. Geneva: World Health Organization [cited 2021 Aug 9]. Available from https://www.who.int/health-topics/obesity#tab=tab_1.

2. Cheymol G. Effects of obesity on pharmacokinetics implications for drug therapy. Clin Pharmacokinet 2000;39:215–31.

3. Pai MP, Paloucek FP. The origin of the “ideal” body weight equations. Ann Pharmacother 2000;34:1066–9.

4. James WP. Research on obesity London: Her Majesty’s Stationery Office; 1976.

5. Janmahasatian S, Duffull SB, Ash S, Ward LC, Byrne NM, Green B. Quantification of lean bodyweight. Clin Pharmacokinet 2005;44:1051–65.

6. Mosteller RD. Simplified calculation of body-surface area. N Engl J Med 1987;317:1098.

7. Shibutani K, Inchiosa MA Jr, Sawada K, Bairamian M. Accuracy of pharmacokinetic models for predicting plasma fentanyl concentrations in lean and obese surgical patients: derivation of dosing weight (“pharmacokinetic mass”). Anesthesiology 2004;101:603–13.

8. Abernethy DR, Burckart GJ. Pediatric dose selection. Clin Pharmacol Ther 2010;87:270–1.

9. Mahmood I. Prediction of clearance, volume of distribution and half-life by allometric scaling and by use of plasma concentrations predicted from pharmacokinetic constants: a comparative study. J Pharm Pharmacol 1999;51:905–10.

10. Mahmood I. Prediction of drug clearance in children: impact of allometric exponents, body weight, and age. Ther Drug Monit 2007;29:271–8.

11. Adams JP, Murphy PG. Obesity in anaesthesia and intensive care. Br J Anaesth 2000;85:91–108.

12. Shenkman Z, Shir Y, Brodsky JB. Perioperative management of the obese patient. Br J Anaesth 1993;70:349–59.

13. Casati A, Putzu M. Anesthesia in the obese patient: pharmacokinetic considerations. J Clin Anesth 2005;17:134–45.

14. Kendrick JG, Carr RR, Ensom MH. Pharmacokinetics and drug dosing in obese children. J Pediatr Pharmacol Ther 2010;15:94–109.

15. Shi S, Klotz U. Age-related changes in pharmacokinetics. Curr Drug Metab 2011;12:601–10.

16. Jung D, Mayersohn M, Perrier D, Calkins J, Saunders R. Thiopental disposition in lean and obese patients undergoing surgery. Anesthesiology 1982;56:269–74.

17. Servin F, Farinotti R, Haberer JP, Desmonts JM. Propofol infusion for maintenance of anesthesia in morbidly obese patients receiving nitrous oxide. A clinical and pharmacokinetic study. Anesthesiology 1993;78:657–65.

18. Lesser GT, Deutsch S. Measurement of adipose tissue blood flow and perfusion in man by uptake of 85Kr. J Appl Physiol 1967;23:621–30.

19. Björkman S, Wada DR, Stanski DR. Application of physiologic models to predict the influence of changes in body composition and blood flows on the pharmacokinetics of fentanyl and alfentanil in patients. Anesthesiology 1998;88:657–67.

20. Avram MJ, Krejcie TC. Using front-end kinetics to optimize target-controlled drug infusions. Anesthesiology 2003;99:1078–86.

21. Collis T, Devereux RB, Roman MJ, de Simone G, Yeh J, Howard BV, et al. Relations of stroke volume and cardiac output to body composition: the strong heart study. Circulation 2001;103:820–5.

22. Abernethy DR, Greenblatt DJ, Divoll M, Smith RB, Shader RI. The influence of obesity on the pharmacokinetics of oral alprazolam and triazolam. Clin Pharmacokinet 1984;9:177–83.

23. Salazar DE, Corcoran GB. Predicting creatinine clearance and renal drug clearance in obese patients from estimated fat-free body mass. Am J Med 1988;84:1053–60.

24. Stokholm KH, Brøchner-Mortensen J, Hoilund-Carlsen PF. Increased glomerular filtration rate and adrenocortical function in obese women. Int J Obes 1980;4:57–63.

25. Benedek IH, Fiske WD 3rd, Griffen WO, Bell RM, Blouin RA, McNamara PJ. Serum alpha 1-acid glycoprotein and the binding of drugs in obesity. Br J Clin Pharmacol 1983;16:751–4.

26. Barbeau P, Litaker MS, Woods KF, Lemmon CR, Humphries MC, Owens S, et al. Hemostatic and inflammatory markers in obese youths: effects of exercise and adiposity. J Pediatr 2002;141:415–20.

27. Derry CL, Kroboth PD, Pittenger AL, Kroboth FJ, Corey SE, Smith RB. Pharmacokinetics and pharmacodynamics of triazolam after two intermittent doses in obese and normal-weight men. J Clin Psychopharmacol 1995;15:197–205.

28. Wasan KM, Lopez-Berestein G. The influence of serum lipoproteins on the pharmacokinetics and pharmacodynamics of lipophilic drugs and drug carriers. Arch Med Res 1993;24:395–401.

29. Lloret Linares C, Declèves X, Oppert JM, Basdevant A, Clement K, Bardin C, et al. Pharmacology of morphine in obese patients: clinical implications. Clin Pharmacokinet 2009;48:635–51.

30. Ramzan I, Wong BK, Corcoran GB. Pain sensitivity in dietary-induced obese rats. Physiol Behav 1993;54:433–5.

31. Maffiuletti NA, Morelli A, Martin A, Duclay J, Billot M, Jubeau M, et al. Effect of gender and obesity on electrical current thresholds. Muscle Nerve 2011;44:202–7.

32. McVinnie DS. Obesity and pain. Br J Pain 2013;7:163–70.

33. Majchrzak M, Brzecka A, Daroszewski C, Blasiak P, Rzechonek A, Tarasov VV, et al. Increased pain sensitivity in obese patients after lung cancer surgery. Front Pharmacol 2019;10:626.

34. Cortínez LI, Anderson BJ, Penna A, Olivares L, Muñoz HR, Holford NH, et al. Influence of obesity on propofol pharmacokinetics: derivation of a pharmacokinetic model. Br J Anaesth 2010;105:448–56.

35. Dong D, Peng X, Liu J, Qian H, Li J, Wu B. Morbid obesity alters both pharmacokinetics and pharmacodynamics of propofol: dosing recommendation for anesthesia induction. Drug Metab Dispos 2016;44:1579–83.

36. Subramani Y, Riad W, Chung F, Wong J. Optimal propofol induction dose in morbidly obese patients: a randomized controlled trial comparing the bispectral index and lean body weight scalar. Can J Anaesth 2017;64:471–9.

37. Cortínez LI, Anderson BJ. Advances in pharmacokinetic modeling: target controlled infusions in the obese. Curr Opin Anaesthesiol 2018;31:415–22.

38. Eleveld DJ, Proost JH, Cortínez LI, Absalom AR, Struys MM. A general purpose pharmacokinetic model for propofol. Anesth Analg 2014;118:1221–37.

39. Vereecke HE, Eleveld DJ, Colin P, Struys MM. Performance of the eleveld pharmacokinetic model to titrate propofol in an obese Japanese patient population. Eur J Anaesthesiol 2016;33:58–9.

40. Aldegheri G, Di Candia D, Gigli F. Predictive performance of the 'Minto' remifentanil pharmacokinetic parameter set in morbidly obese patients ensuing from a new method for calculating lean body mass. Clin Pharmacokinet 2010;49:131–9.

41. La Colla L, Albertin A, La Colla G. Pharmacokinetic model-driven remifentanil administration in the morbidly obese: the ‘critical weight’ and the ‘fictitious height’, a possible solution to an unsolved problem? Clin Pharmacokinet 2009;48:397–8.

42. Kim TK, Obara S, Egan TD, Minto CF, La Colla L, Drover DR, et al. Disposition of remifentanil in obesity: a new pharmacokinetic model incorporating the influence of body mass. Anesthesiology 2017;126:1019–32.

43. Cortínez LI, De la Fuente N, Eleveld DJ, Oliveros A, Crovari F, Sepulveda P, et al. Performance of propofol target-controlled infusion models in the obese: pharmacokinetic and pharmacodynamic analysis. Anesth Analg 2014;119:302–10.

44. Eleveld DJ, Colin P, Absalom AR, Struys MM. Pharmacokinetic-pharmacodynamic model for propofol for broad application in anaesthesia and sedation. Br J Anaesth 2018;120:942–59.

45. Bouillon TW, Bruhn J, Radulescu L, Andresen C, Shafer TJ, Cohane C, et al. Pharmacodynamic interaction between propofol and remifentanil regarding hypnosis, tolerance of laryngoscopy, bispectral index, and electroencephalographic approximate entropy. Anesthesiology 2004;100:1353–72.

46. Yufune S, Takamatsu I, Masui K, Kazama T. Effect of remifentanil on plasma propofol concentration and bispectral index during propofol anaesthesia. Br J Anaesth 2011;106:208–14.

47. Yi JM, Doh I, Lee SH, Kim SY, Lee YH, Lee EK, et al. Predictive performance of a new pharmacokinetic model for propofol in underweight patients during target-controlled infusion. Acta Anaesthesiol Scand 2019;63:448–54.

48. Gutt CN, Oniu T, Mehrabi A, Schemmer P, Kashfi A, Kraus T, et al. Circulatory and respiratory complications of carbon dioxide insufflation. Dig Surg 2004;21:95–105.

49. Nguyen NT, Ho HS, Fleming NW, Moore P, Lee SJ, Goldman CD, et al. Cardiac function during laparoscopic vs open gastric bypass. Surg Endosc 2002;16:78–83.

50. Perilli V, Sollazzi L, Modesti C, Annetta MG, Sacco T, Bocci MG, et al. Comparison of positive end-expiratory pressure with reverse Trendelenburg position in morbidly obese patients undergoing bariatric surgery: effects on hemodynamics and pulmonary gas exchange. Obes Surg 2003;13:605–9.

51. Shibutani K, Inchiosa MA Jr, Sawada K, Bairamian M. Pharmacokinetic mass of fentanyl for postoperative analgesia in lean and obese patients. Br J Anaesth 2005;95:377–83.

Article information Continued

This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Dosing scalar	Equation
Ideal body weight	Males: 50 kg + 2.3 kg for each 2.54 cm (1 in) over 152 cm (5 ft)
Ideal body weight	Females: 45.5 kg + 2.3 kg for each 2.54 cm (1 in) over 152 cm (5 ft)
Lean body weight	Males: 1.1 × TBW − 128 × (TBW / Ht)²
Lean body weight	Females: 1.07 × TBW − 148 × (TBW / Ht)²
Fat-free mass [5]	Males: (9.27 × 10³ × TBW) / (6.68 × 10³ + 216 × BMI)
Fat-free mass [5]	Females: (9.27 × 10³ × TBW) / (8.78 × 10³ + 244 × BMI)
Body surface area (Mosteller’s adaptation) [6]	[(height [cm] - TBW) / 3600]^1/2
Pharmacokinetic mass [7,51]	52 / [1 + (196.4 × e^{-0.025 TBW} − 53.66) / 100] (fentanyl only)
Corrected body weight or Adjusted body weight [17,34]	IBW + 0.4 × (TBW – IBW)
Allometric scaling	With allometric coefficient alpha, clearance = beta × (TBW)^alpha