Assessment of P values for demographic data in randomized controlled trials
Article information
Abstract
In a large number of randomized controlled trials, researchers provide P values for demographic data, which are commonly reported in table 1 of the article for the purpose of emphasizing the lack of differences between or among groups. As such, the authors intend to demonstrate that statistically insignificant P values in the demographic data confirm that group randomization was adequately performed. However, statistically insignificant P values do not necessarily reflect successful randomization. It is more important to rigorously establish a plan for statistical analysis during the design and planning stage of the study, and to consider whether any of the variables included in the demographic data could potentially affect the research results. If a researcher rigorously designed and planned a study, and performed it accordingly, the conclusions drawn from the results would not be influenced by P values, regardless of whether they were significant. In contrasts, imbalanced variables could affect the results after variance controlling, even though whole study process are well planned and executed. In this situation, the researcher can provide results with both the initial method and a second stage of analysis including such variables. Otherwise, for brief conclusions, it would be pointless to report P values in a table simply listing baseline data of the participants.
Pre-occupation with P values for Baseline Characteristics
The statistical tests used to compare baseline data in randomized controlled trials have remained questionable since 1990. In studies investigating baseline balance in clinical trials, Roberts and Torgerson [1], and Senn [2] suggested that significance tests to detect baseline differences are inappropriate. In 1990, 41% of randomized controlled trial (RCT)s reported inadequate comparisons of baseline characteristics [3]. One-half of the trials published in 1997 assessed imbalances between treatment groups using significant tests [4]. In addition, there are different rules among the major journals and the CONSORT guidelines for reporting P values comparing baseline characteristics. The New England Journal of Medicine mandates statistical tests with P values for baseline characteristics.1) Otherwise, CONSORT 2010 discourages statistical tests of baseline characteristics with the following comment: “Such significance tests assess the probability that observed baseline differences could have occurred by chance; however, we already know that any differences are caused by chance. Tests of baseline differences are not necessarily wrong, just illogical.”2)
In several studies designed and performed as a RCT, baseline data, such as demographics, medical history, vital signs and measurements, are usually collected. There are several reasons for collecting baseline data. First, the data provide information about the characteristics of the included patients. Second, baseline data show that the groups are well balanced by comparing groups, especially with critical variables that may significantly influence the results. Third, subgroup analyses may be performed on selected patient characteristics, which can also influence the results. Finally, covariate adjustment may be used to account for particular baseline factors.
Randomization is performed to avoid systematic errors that may occur during group assignment [5]. However, randomization cannot always prevent imbalances between two groups; more specifically, statistically significant differences in baseline data could occur by chance after randomization.
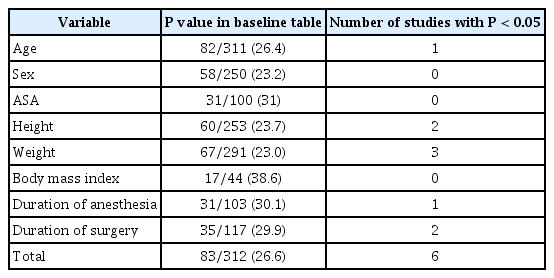
For example, if an RCT has 2 groups and 30 subjects, including both sexes, in each group, when randomization is conducted in such a study, the probability of a statistically significant difference (i.e., P < 0.05) in the sex variable is 0.0519. Of all studies published in the Korean Journal of Anesthesiology (KJA) between 2010 and 2017, 58 reported a P value for the sex variable (Table 1). Assuming these 58 studies have same number of groups and subjects in each group, the probability of all studies to reporting a statistically insignificant difference is (1−0.0519)58. This value is 0.045451 and is statistically significant (P < 0.05). Moreover, 2.6 of 58 studies are expected to reveal a statistically significant difference in the sex variable. From 8 variable categories, 318 variables reported P values (Table 1). From these 318 variables, only 9 reported statistically significant difference. However, assuming 318 variables have same number of groups and subjects, and also the same probability of a statistically significant difference between groups, the possibility of reporting a statistical difference ≤ 9 is 0.004812.
The most inappropriate scientific point is that the null hypothesis against randomization is never proven during statistical analysis of baseline variables. That is, P values presented to contend the balanced baseline parameters have not enough evidences to reject the null hypothesis, imbalanced variables between groups.
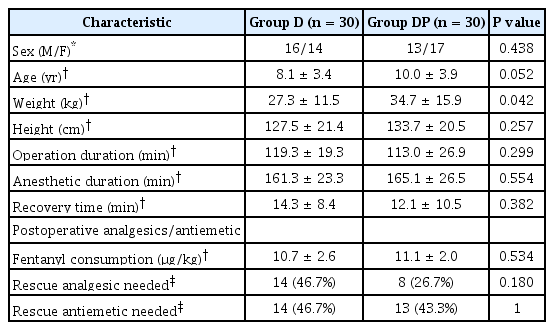
The P value may also be partially influenced by sample size. In a small study, the P value may not reach statistical significance, even when there is a clinically relevant difference in a given baseline characteristic. For example, as shown in Table 2 [6], patient ages are not statistically different (8.1 [3.4] versus 10.0 [3.9]; P = 0.052). However, an almost 2-year gap in a group of pediatric patients could have a meaningful effect on the result in a clinical situation. Furthermore, a larger number of subjects would increase the possibility of obtaining smaller P values. Therefore, the authors suggest that the P values usually reported in Table 1 have no practicable meaning, but do afford the chance to incorrectly interpret the results of studies.
P values Published in the KJA
A total of 312 RCTs were published in the KJA from 2010 to 2017, and were reviewed. In most studies, patient baseline characteristics, such as age, sex, American Society of Anesthesiologists (ASA) physical status classification, height, weight, body mass index (BMI), duration of anesthesia and duration of the operation, that fulfilled inclusion criteria, were described in the baseline tables. Therefore, the baseline tables in each article, in terms of these eight variables, were reviewed. As shown in Table 1, 82 of the 312 studies reported a P value when comparing ages between or among groups, while 58 reported P values for comparisons of sex between or among groups. Respectively, 31, 60, 67, 17, 31, and 35 of the 312 RCTs reported P values for comparisons of ASA, height, weight, BMI, duration of anesthesia and surgery. Eighty-three (26.5%) studies reported P values in baseline data tables, among which 6 [6–11] reported P values that were statistically significant (i.e., < 0.05). Descriptions such as “similar” or “comparable” in the article were not considered as significant. Among the 6 studies that reported P values, variables that demonstrated significant differences were controlled for 2 investigations. In the study by Shin et al. [10], groups were divided according to age. In the study by Kim et al. [9] groups were divided according to the type of surgery, which could have possibly caused a difference in the duration of the operation and anesthesia between the groups.
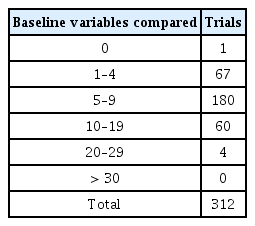
The number of baseline variables varied widely, from 0 to 23 (Table 3). One study [12] did not report baseline characteristics of the included patients. In this study, the baseline table presented information only about the assessment of intubation conditions, including ease of laryngoscopy, vocal cord position and vocal cord movement, among others. More than one-half (57.7%) of the included studies reported 5 to 9 baseline variables.
How to Improve the Assessment of Balance in Baseline Characteristics of Clinical Trial Participants?
It would be ideal if studies recruited subjects with little-tono heterogeneity between and among groups through rigorous methodology design, careful planning and study execution, and additionally, the inclusion of a large sample size. Furthermore, researchers could gather pilot patient data to determine whether they present any risk of bias or imbalance in baseline information between groups before designing and planning the study. However, these processes are often cost prohibitive, and involve large consumption of human and time resources. For these limitations, researchers could perform statistical interventions.
Statistical conclusions leave little room for doubt, but only if the baseline variables are well randomized and do not influence the results of the study. However, if there are any risks of influencing patient outcomes, these risks for bias on statistical outcomes may be of great concern [2].
How can variables that have the potential to affect study results be controlled? The researcher should review whether adequate and appropriate randomization has been performed. Randomization reduces risk for confounding by generating groups that are fairly comparable with regard to known and unknown confounding variables [13]. However, as mentioned above, randomization does not always prevent imbalance between two groups; therefore, to control imbalances in baseline data, several strategies can be applied.
First, restriction can eliminate variation in the confounder. Inclusion criteria could be restricted to a certain population of interest in the design and planning stages of the study [13]. For example, female is a risk factor for postoperative nausea and vomiting (PONV). If the researcher plans to study the relationship between a drug and PONV, the influence of this variable (i.e., sex) in the results may disappear by including only female subjects. Furthermore, including only elderly patients or infants in studies can control the influence of age on the study result(s).
Second, stratified randomization could help to prevent confounding variables that cause bias by chance with the help of generating strata before randomization. For example, when patient age is anticipated to be a highly important factor that may affect the results, the age of the included patients can be stratified into several groups (e.g., group 1, 20–40; group 2, 40–60; group 3, 60–80; group 4, > 80 years of age). Stratification can help mitigate the level of confounding and produce groups in which the confounder does not vary [13]. However, stratification could also cause the size of subgroups to be smaller (data thinning).
Third, covariate adaptive randomization helps to prevent imbalance in important covariates that could affect study outcomes. Covariate adaptive randomization assigns new subjects to the treatment groups, taking into account the covariates of previously assigned subjects to the treatment groups [14].
Finally, statistical methods that adjust for possible covariates, such as analysis of covariance (ANCOVA) or multivariate analysis of covariance (MANCOVA), can be used. These methods, which adjust for a highly prognostic covariate, can improve precision. Covariates should be chosen on the basis of their possible correlation with variable and outcomes, regardless of whether the baseline data exhibit “imbalances in statistical tests.” Covariates should be chosen during the design and planning stages of studies with thorough consideration. If chosen, a covariate must be adjusted for, regardless of whether imbalances are observed. Even if there is little imbalance, adjustment of covariates will result in smaller standard errors, tighter confidence intervals, and more powerful significance tests. However, if it performed without consideration during the design and planning stages of the study, typical methods for estimating standard errors will incorrectly assume that the investigators never controlled for the variable, regardless of the extent of imbalance observed. Additionally, sample size of the study should be calculated based on the planned method of statistical analysis [15].
Most importantly, all of the methods mentioned above should be concretely established at the design and planning stages of the study, and should be included in the statistical analysis plan. If statistical imbalance in baseline characteristics arises, and the researchers missed all the methods mentioned above, the researcher may be questioned by reviewers or readers whether the outcome has been influenced by the imbalance in baseline characteristics. In such circumstances, an additional/supplemental adjusted analysis can be performed, considering the imbalance in baseline characteristics. The researcher can imitate the adjustment for all variables that were identified as prognostic factors in advance. If both adjusted and unadjusted analyses yield the same results, interpretation is achieved without difficulty and the conclusions would be accepted without dispute. However, if adjusted and unadjusted analyses yield different results, there could be a debate about certain results and their proper interpretation. In such cases, the results from statistical methods that are pre-planned in the statistical analysis plan should be taken primarily [16]. If the study was well conducted according to the pre-planned statistical methodology, the authors suggest that imbalances in data could be considered to have been caused by chance. In addition, bias is not expected to be serious if investigators pre-plan the statistical method, analyze data according to pre-planned statistical method and be forthcoming and transparent in describing the limitations of the study in the discussion section [17].
In conclusion, the authors suggest that authors should try to apply strategies to control the imbalance for possible confounders in the design and planning stages of the study rather than reporting P values for baseline data in RCTs for the purposes of demonstrating that the randomization process was adequate.
Notes
http://www.nejm.org/page/author-center/manuscript-submission [accessed November 21, 2018]
http://www.consort-statement.org/checklists/view/32-consort/510-baseline-data [accessed November 21, 2018]
Notes
No potential conflict of interest relevant to this article was reported.
Author Contributions
Eun Jin Ahn (Data curation; Investigation; Methodology; Writing – original draft; Writing – review & editing)
Jong Hae Kim (Data curation; Investigation; Writing – review & editing)
Tae Kyun Kim (Data curation; Investigation; Writing – review & editing)
Jae Hong Park (Data curation; Investigation; Writing – review & editing)
Dong Kyu Lee (Conceptualization; Data curation; Methodology; Writing – review & editing)
Sangseok Lee (Conceptualization; Data curation; Investigation; Writing – review & editing)
Junyong In (Data curation; Investigation; Writing – review & editing)
Hyun Kang (Conceptualization; Data curation; Formal analysis; Funding acquisition; Investigation; Methodology; Project administration; Resources; Software; Supervision; Validation; Visualization; Writing – original draft; Writing – review & editing)