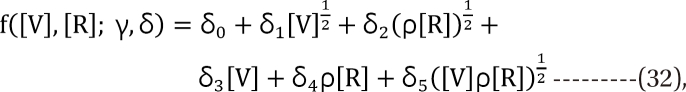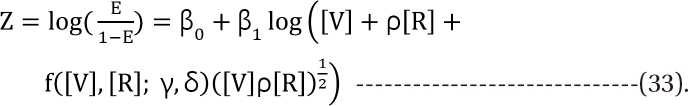1. Chou TC. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in drug combination studies. Pharmacol Rev 2006; 58: 621-681. PMID:
16968952.


2. Hendrickx JF, Eger EI 2nd, Sonner JM, Shafer SL. Is synergy the rule? A review of anesthetic interactions producing hypnosis and immobility. Anesth Analg 2008; 107: 494-506. PMID:
18633028.


3. Johnson KB, Syroid ND, Gupta DK, Manyam SC, Pace NL, Lapierre CD, et al. An evaluation of remifentanil-sevoflurane response surface models in patients emerging from anesthesia: model improvement using effect-site sevoflurane concentrations. Anesth Analg 2009;[Epub ahead of print].

4. Syroid ND, Johnson KB, Pace NL, Westenskow DR, Tyler D, Bruhschwein F, et al. Response surface model predictions of emergence and response to pain in the recovery room: an evaluation of patients emerging from an isoflurane and fentanyl anesthetic. Anesth Analg 2009;[Epub ahead of print].

5. Schumacher PM, Dossche J, Mortier EP, Luginbuehl M, Bouillon TW, Struys MM. Response surface modeling of the interaction between propofol and sevoflurane. Anesthesiology 2009; 111: 790-804. PMID:
19741484.


6. Naguib M, Abdulatif M. Isobolographic and dose-response analysis of the interaction between pipecuronium and vecuronium. Br J Anaesth 1993; 71: 556-560. PMID:
7903151.


7. Redai I, Richards KM, England AJ, Feldman SA. Interaction of decamethonium with hexamethonium or vecuronium in the rat: an isobolographic analysis. Anesth Analg 1995; 81: 768-772. PMID:
7574008.

8. Paul M, Kindler CH, Fokt RM, Dipp NC, Yost CS. Isobolographic analysis of non-depolarising muscle relaxant interactions at their receptor site. Eur J Pharmacol 2002; 438: 35-43. PMID:
11906708.


9. Berenbaum MC. What is synergy? Pharmacol Rev 1989; 41: 93-141. PMID:
2692037.

10. Greco WR, Bravo G, Parsons JC. The search for synergy: a critical review from a response surface perspective. Pharmacol Rev 1995; 47: 331-385. PMID:
7568331.

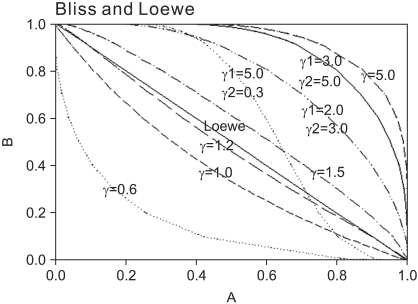
11. Bliss CI. The toxicity of poisons applied jointly. Ann Appl Biol 1939; 26: 585-615.

12. Loewe S. The problem of synergism and antagonism of combined drugs. Arzneimittelforschung 1953; 3: 285-290. PMID:
13081480.

13. Chou TC. Drug combination studies and their synergy quantification using the chou-talalay method. Cancer Res 2010; 70: 440-446. PMID:
20068163.


14. Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol (Lond) 1910; 40: iv-vii.
15. Sheiner LB, Stanski DR, Vozeh S, Miller RD, Ham J. Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharmacol Ther 1979; 25: 358-371. PMID:
761446.


16. Chou TC, Talalay P. Quantitative analysis of dose-effect relationships: the combined effects of multiple drugs or enzyme inhibitors. Adv Enzyme Regul 1984; 22: 27-55. PMID:
6382953.


17. Berenbaum MC. Criteria for analyzing interactions between biologically active agents. Adv Cancer Res 1981; 35: 269-335. PMID:
7041539.


18. Fraser TR. An experimental research on the antagonism between the actions of physostigma and atropia. Proc R Soc Edingburgh 1870-1; 7: 506-511.

20. Loewe S, Muischnek H. Effect of combinations: mathematical basis of problem. Arch Exp Pathol Pharmakol 1926; 114: 313-326.

21. Tallarida RJ. An overview of drug combination analysis with isobolograms. J Pharmacol Exp Ther 2006; 319: 1-7. PMID:
16670349.


22. Grabovsky Y, Tallarida RJ. Isobolographic analysis for combinations of a full and partial agonist: curved isoboles. J Pharmacol Exp Ther 2004; 310: 981-986. PMID:
15175417.


23. Tallarida RJ. Interactions between drugs and occupied receptors. Pharmacol Ther 2007; 113: 197-209. PMID:
17079019.


24. Chou TC. Derivation and properties of michaelis-menten type and hill type equations for reference ligands. J Theor Biol 1976; 59: 253-276. PMID:
957690.


25. Chou TC. On the determination of availability of ligand binding sites in steady-state systems. J Theor Biol 1977; 65: 345-356. PMID:
853753.


26. Berenbaum MC. Synergy, additivism and antagonism in immunosuppression. A critical review. Clin Exp Immunol 1977; 28: 1-18. PMID:
324671.


27. Goldoni M, Johansson C. A mathematical approach to study combined effects of toxicants in vitro: evaluation of the bliss independence criterion and the loewe additivity model. Toxicol In Vitro 2007; 21: 759-769. PMID:
17420112.


28. Fitzgerald JB, Schoeberl B, Nielsen UB, Sorger PK. Systems biology and combination therapy in the quest for clinical efficacy. Nat Chem Biol 2006; 2: 458-466. PMID:
16921358.


29. Martinez-Irujo JJ, Villahermosa ML, Mercapide J, Cabodevilla JF, Santiago E. Analysis of the combined effect of two linear inhibitors on a single enzyme. Biochem J 1998; 329: 689-698. PMID:
9445400.



30. Lee JJ, Kong M, Ayers GD, Lotan R. Interaction index and different methods for determining drug interaction in combination therapy. J Biopharm Stat 2007; 17: 461-480. PMID:
17479394.


31. Gessner PK. Isobolographic analysis of interactions: an update on applications and utility. Toxicology 1995; 105: 161-179. PMID:
8571354.


32. Mead R, Pike DJ. A biometrics invited paper. A review of response surface methodology from a biometric viewpoint. Biometrics 1975; 31: 803-851. PMID:
1106790.


33. Finney DJ. Probit Analysis. 1971, 3rd ed. Cambridge, UK, Cambridge University Press.
34. Greco WR, Park HS, Rustum YM. Application of a new approach for the quantitation of drug synergism to the combination of cis-diamminedichloroplatinum and 1-beta-D-arabinofuranosylcytosine. Cancer Res 1990; 50: 5318-5327. PMID:
2386940.

35. Machado SG, Robinson GA. A direct, general approach based on isobolograms for assessing the joint action of drugs in pre-clinical experiments. Stat Med 1994; 13: 2289-2309. PMID:
7855464.


36. Plummer JL, Short TG. Statistical modeling of the effects of drug combinations. J Pharmacol Methods 1990; 23: 297-309. PMID:
2196402.


37. Carter WH, Gennings C, Staniswalis JG, Campbell ED, White KL. A statistical approach to the construction and analysis of isobolograms. Int J Toxicol 1988; 7: 963-973.

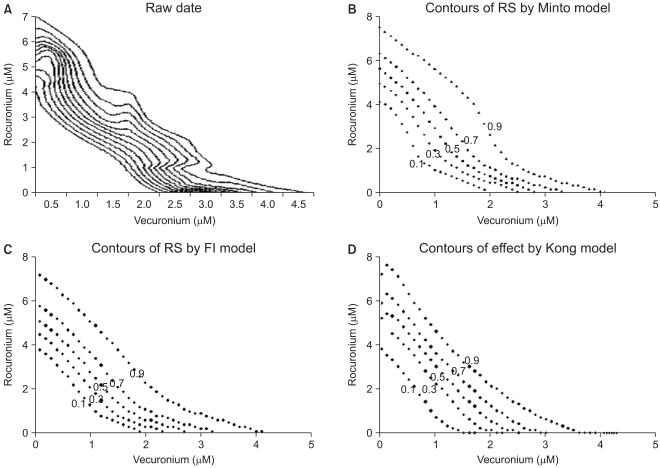
38. Kong M, Lee JJ. A generalized response surface model with varying relative potency for assessing drug interaction. Biometrics 2006; 62: 986-995. PMID:
17156272.


39. Minto CF, Schnider TW, Short TG, Gregg KM, Gentilini A, Shafer SL. Response surface model for anesthetic drug interactions. Anesthesiology 2000; 92: 1603-1616. PMID:
10839909.


40. Fidler M, Kern SE. Flexible interaction model for complex interactions of multiple anesthetics. Anesthesiology 2006; 105: 286-296. PMID:
16871062.



41. Hewlett PS. Measurement of the potencies of drug mixtures. Biometrics 1969; 25: 477-487. PMID:
5824400.


42. Plackett RL, Hewlett PS. Quantal responses to mixtures of poisons. J R Stat Soc Series B Stat Methodol 1952; 14: 141-163.

43. Cox DR. The analysis of multivariate binary data. Applied Statistics 1972; 21: 113-120.

44. Gennings C, Carter WH Jr, Campbell ED, Staniswalis JG, Martin TJ, Martin BR, et al. Isobolographic characterization of drug interactions incorporating biological variability. J Pharmacol Exp Ther 1990; 252: 208PMID:
2299590.

45. Chou TC, Hayball M. CalcuSyn for Windows: Multiple-Drug Dose-Effect Anayzer and Manual. 1996, Cambridge, United Kingdom, Biosoft, Cambridge Place.
46. Burnham KP, Anderson DR. Model selection and multimodel inference: a practical information-theoretic approach. 2002, 2nd ed. New York, USA, pp 1-488.
47. Weakliem DL. Introduction to the special issue on model selection. Sociol Methods Res 2004; 33: 167.

48. Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr 1974; 19: 716-723.

49. Schwarz G. Estimating the dimension of a model. Ann Stat 1978; 6: 461-464.

50. Reschenhofer E. Prediction with vague prior knowledge. Commun Stat Theory Methods 1996; 25: 601-608.

51. Kullback S. The kullback-leibler distance. Am Stat 1987; 41: 340-341.
52. Kullback S, Leibler RA. On information and sufficiency. Ann Math Statist 1951; 22: 79-86.

53. Babyak MA. What you see may not be what you get : a brief, nontechnical introduction to overfitting in regression-type models. Psychosom Med 2004; 66: 411-421. PMID:
15184705.


54. Concato J, Peduzzi P, Holford TR, Feinstein AR. Importance of events per independent variable in proportional hazards analysis. I. background, goals, and general strategy. J Clin Epidemiol 1995; 48: 1495-1501. PMID:
8543963.


55. Peduzzi P, Concato J, Feinstein AR, Holford TR. Importance of events per independent variable in proportional hazards regression analysis. II. accuracy and precision of regression estimates. J Clin Epidemiol 1995; 48: 1503-1510. PMID:
8543964.



56. Peduzzi P, Concato J, Kemper E, Holford TR, Feinstein AR. A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol 1996; 49: 1373-1379. PMID:
8970487.


57. Burnham KP, Anderson DR. Multimodel inference: understanding AIC and BIC in model selection. Sociol Methods Res 2004; 33: 261.



 is a fraction of the effect resulting from the mixture of d1 and d2; d1 and d2 are doses of each drug in the mixture that yield the effect E; ED50,1 or 2 is a dose of drugs to produce 50% of the maximal effect (Emax) for each drug acting alone; and ╬│1 and ╬│2 are Hill coefficients (slope of dose-response curve). When Eq. (1) and (2) are recast in terms of the fraction of effect affected (fa1 or 2) (if 1 - fa exchanges fu in Eq. (1), because fa + fu = 1), then Eq. (3) and (4) are the results.
is a fraction of the effect resulting from the mixture of d1 and d2; d1 and d2 are doses of each drug in the mixture that yield the effect E; ED50,1 or 2 is a dose of drugs to produce 50% of the maximal effect (Emax) for each drug acting alone; and ╬│1 and ╬│2 are Hill coefficients (slope of dose-response curve). When Eq. (1) and (2) are recast in terms of the fraction of effect affected (fa1 or 2) (if 1 - fa exchanges fu in Eq. (1), because fa + fu = 1), then Eq. (3) and (4) are the results.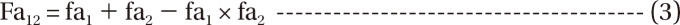


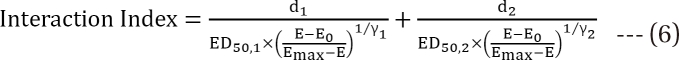
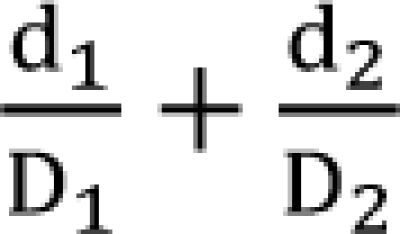 is called the interaction index at the combination dose (d1, d2). The dose (D1, or D2) for each single drug producing the same effect of E is expressed as
is called the interaction index at the combination dose (d1, d2). The dose (D1, or D2) for each single drug producing the same effect of E is expressed as

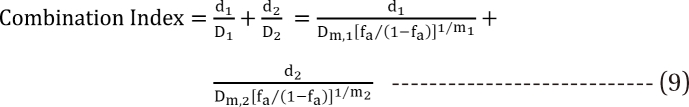


 ,
, 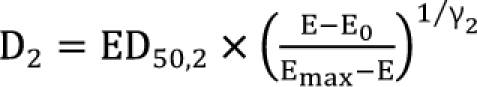 , the first two terms on the right-hand expression of Eq. (11) are equivalent to Eq. (5). Thus, Eq. (12) defines interaction index for two-drug combination.
, the first two terms on the right-hand expression of Eq. (11) are equivalent to Eq. (5). Thus, Eq. (12) defines interaction index for two-drug combination.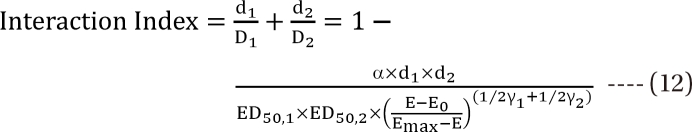


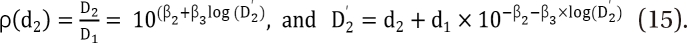
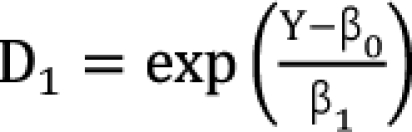 ,
,  which are the doses of drug 1 and drug 2 producing the effect E. You can rearrange Eq. (14) to be
which are the doses of drug 1 and drug 2 producing the effect E. You can rearrange Eq. (14) to be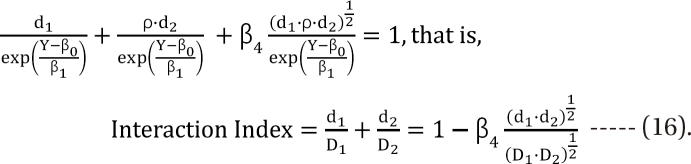
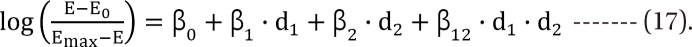
 ,
, 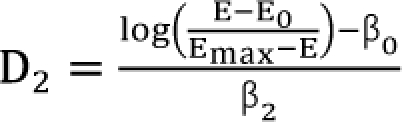 . After moving ╬▓0 to the left side of Eq. (17), and then dividing both sides of the equation with
. After moving ╬▓0 to the left side of Eq. (17), and then dividing both sides of the equation with 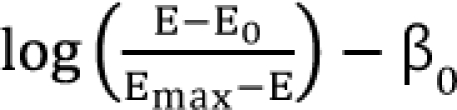 , you will obtain the interaction index:
, you will obtain the interaction index: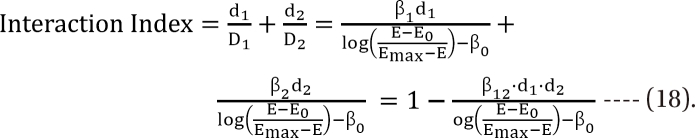

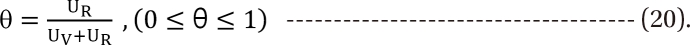


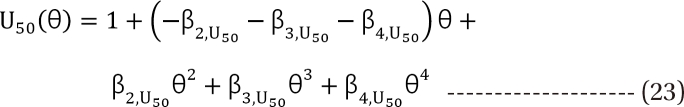
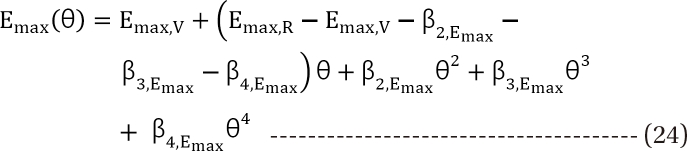

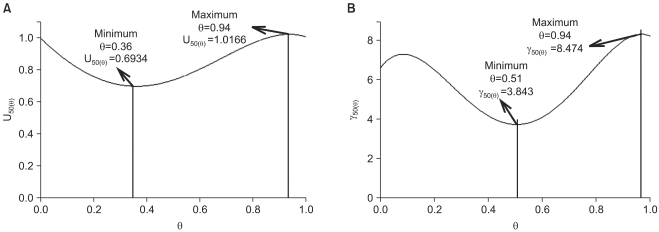
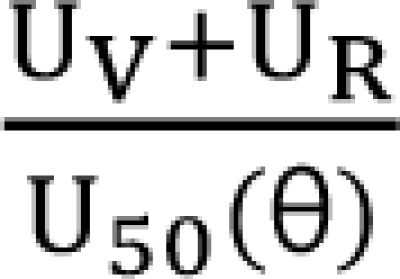 in Eq. (21). This will create a synergistic effect. If U50(╬Ė) is greater than 1 for all values of ╬Ė, this lessen the term
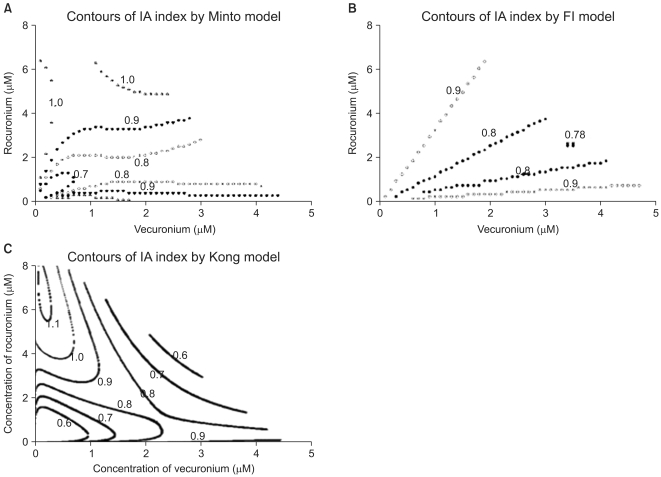
in Eq. (21). This will create a synergistic effect. If U50(╬Ė) is greater than 1 for all values of ╬Ė, this lessen the term 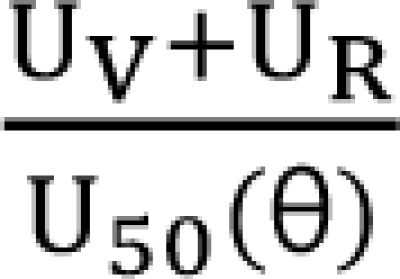 in Eq. (21). This will create an antagonistic effect. This model can be used in investigating the drug interaction when the maximum effects of drugs V and R are not identical.
in Eq. (21). This will create an antagonistic effect. This model can be used in investigating the drug interaction when the maximum effects of drugs V and R are not identical.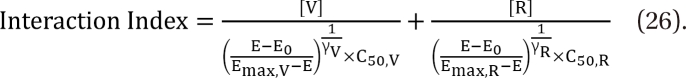


 ,
, 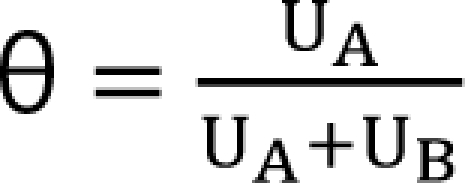 . The m term is the symmetry parameter of the potency ratio ╬Ė, where the maximum interaction occurs. The interaction scope parameter w specifies the uniformity of the interaction across various drug ratios. The parameters ╬│(╬Ė) and Emax(╬Ė) are given as functions of potency fraction:
. The m term is the symmetry parameter of the potency ratio ╬Ė, where the maximum interaction occurs. The interaction scope parameter w specifies the uniformity of the interaction across various drug ratios. The parameters ╬│(╬Ė) and Emax(╬Ė) are given as functions of potency fraction: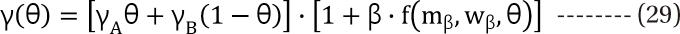
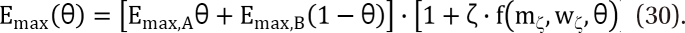
 ) expresses % change of the 50% effect when compared with each drug in combination acting alone. Another feature is for the Fidler model to predict the concentration ratio of two drugs at the most effective points. In an asymmetric case, the best ratio is C50,V ├Ś m : C50,R ├Ś (1 - m); in a symmetric case, the best ratio is C50,V : C50,R.
) expresses % change of the 50% effect when compared with each drug in combination acting alone. Another feature is for the Fidler model to predict the concentration ratio of two drugs at the most effective points. In an asymmetric case, the best ratio is C50,V ├Ś m : C50,R ├Ś (1 - m); in a symmetric case, the best ratio is C50,V : C50,R. . It is assumed that the logit-transformed response follows a linear function of log (d) for each of two drugs when acting independently. The dose-response curve denotes
. It is assumed that the logit-transformed response follows a linear function of log (d) for each of two drugs when acting independently. The dose-response curve denotes 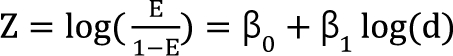 . The model proposed by Kong and Lee has a square root term and the relative potency. So, it can be regarded as a generalization of Finney's model [33] and the model derived by Plummer and Short [36]. To construct a generalized model, including the nonparallel dose-response curves of two drugs, a varying relative potency should be allowed. When the two drugs have the nonparallel dose-response curves, or different slopes, each drug combination ([V], [R]) on the z-isobole shares the same relative potency Žü(z), and its equivalent amount dose is [V] + Žü(z) [R] in terms of drug V, or Žü(z)-1 [V] + [R] in terms of drug R. That is, the combination doses on different isoboles may have different relative potencies. The form of Žü(z) is derived as
. The model proposed by Kong and Lee has a square root term and the relative potency. So, it can be regarded as a generalization of Finney's model [33] and the model derived by Plummer and Short [36]. To construct a generalized model, including the nonparallel dose-response curves of two drugs, a varying relative potency should be allowed. When the two drugs have the nonparallel dose-response curves, or different slopes, each drug combination ([V], [R]) on the z-isobole shares the same relative potency Žü(z), and its equivalent amount dose is [V] + Žü(z) [R] in terms of drug V, or Žü(z)-1 [V] + [R] in terms of drug R. That is, the combination doses on different isoboles may have different relative potencies. The form of Žü(z) is derived as